Erwartungshorizont Symbole und Einheiten

Größe	Typisches Symbol	Einheit
Länge	$s$ (oder $L$)	$\si{\meter}$
Zeit	$t$	$\si{\second}$
Beschleunigung	$a$	$\si{\meter\per\square\second}$
Masse	$m$	$\si{\kilo\gram}$
Kraft	$F$	$\si{\newton} = \si{\kilo\gram\meter\per\square\second}$
Temperatur	$T$	$\si{\kelvin}$

Ergänzungen

Da in der Aufgabenstellung nicht explizit nach den SI-Basiseinheiten beziehungsweise nach abgeleiteten Einheiten, d. h. Potenzprodukte der Basiseinheiten gefragt ist, sind auch andere Einträge in der letzten Spalte möglich. So könnte für die Länge auch $\si{\kilo\meter}$ angegeben werden, eine sogenannte nicht kohärente SI-Einheit. Für die Zeit könnte auch $\si{\hour}$ angegeben werden, eine zur Verwendung mit dem SI zugelassene Einheit. Zu $\si{\kilo\gram}$ sei angemerkt, dass dies die kohärente SI-Einheit der Basisgröße Masse ist, die einzige Basiseinheit mit einem Vorsatz (Präfix). Das $\si{\newton}$ ist eine der 22 abgeleiteten SI-Einheiten mit besonderem Namen, die wichtigsten sollten bekannt sein. Zu diesen wird auch Radiant, $\si{\radian}$ oder das Grad Celsius gezählt, $\si{\celsius}$. Das Winkelgrad, $\si{\degree}$ ist wiederum eine zugelassene Einheit. Eine möglichst gute Kenntnis dieser wichtigen Zusammenhänge wäre wünschenswert, aber das Wissen um alle Einzelheiten übersteigt natürlich die Mindestanforderungen.

Erwartungshorizont Größengleichung

Die Berechnungsformel für die Energie wird nach der Geschwindigkeit aufgelöst: $$\begin{aligned} & & E_{\mathrm{kin}} &= \frac{1}{2} \cdot m \cdot v^2 & &\left| \quad \cdot \frac{2}{m} \right. \\ &\Leftrightarrow & v^2 &= \frac{2 \cdot E_{\mathrm{kin}}}{m} & &\left| \quad \text{Wurzel ziehen} \right.\\ &\Leftrightarrow & v &= \pm \sqrt{\frac{2 \cdot E_{\mathrm{kin}}}{m}} \; .& &\end{aligned}$$ Für den Betrag der Geschwindigkeit gilt das positive Vorzeichen.

Ergänzungen

Das Auflösen der ersten Gleichung nach $v^2$ sollte gekonnt werden. Was kann üblicherweise für den letzten Schritt erwartet werden?

Grundsätzlich sollte bekannt sein, dass die Geschwindigkeit eine vektorielle Größe ist und in die kinetische Energie als skalare Größe nur der Betrag der Geschwindigkeit eingeht, genauer das Skalarprodukt der Geschwindigkeit mit sich selbst. Es wäre gut zu wissen, dass $v$ hier also grundsätzlich den Betrag der Geschwindigkeit bezeichnet, wie er beispielsweise vom Fahrradcomputer gemessen wird, und dass Beträge positive Größen sind.

Wie wäre eine Lösung mit beiden Vorzeichen und einem Hinweis der Art "vorwärts oder rückwärts" zu bewerten? Da es hier keine allgemeingültige Vereinbarung gibt, sollte diese Antwort ebenfalls als richtig gewertet werden, siehe auch Anhang 8.

Erwartungshorizont Einheitenumrechnung

In der ersten Teilaufgabe sollen Angaben unter Beibehaltung der jeweils verwendeten Einheitenkombination – wie zum Beispiel $[\text{Masseneinheit}] / [\text{Längeneinheit}]^3$ oder $[\text{Längeneinheit}] / [\text{Zeiteinheit}]$ – in eine andere Größenordnung umgerechnet werden. Bei der zweiten Teilaufgabe sollen die Größenangaben statt mit der jeweils verwendeten Einheitenkombination nach Umrechnung unter Verwendung der passenden SI-Einheit mit besonderem Namen erfolgen.

1. Eine Dichte von $\SI{7,2}{\gram\per\centi\meter\cubed}$ in $\si{\kilogram\per\cubic\meter}$: $$\SI[per-mode=fraction]{7,2}{\gram\per\centi\meter\cubed} = \num{7,2}\cdot\frac{\SI{1e-03}{\kilogram}}{(\SI{1e-02}{\meter})^3} = \num{7,2}\cdot\frac{\SI{1e-03}{\kilogram}}{\SI{1e-06}{\cubic\meter}} = \SI[per-mode=fraction]{7,2e03}{\kilogram\per\cubic\meter} \; .$$

   Eine Fläche von $\SI{1,65}{\square\meter}$ in $\si{\centi\meter\squared}$: $$\SI{1,65}{\square\meter} = \num{1,65} \cdot (\SI{100}{\centi\meter})^2 = \num{1,65} \cdot (\SI{1e02}{\centi\meter})^2 = \num{1,65} \cdot \SI{1e04}{\centi\meter\squared} \; .$$

   Eine Zeitdauer von $\SI{3,5}{\hour}$ in $\si{\minute}$: $$\SI{3,5}{\hour} = \num{3,5} \cdot \SI{60}{\minute} = \SI{210}{\minute} \; .$$

   Eine Geschwindigkeit von $\SI{0,018}{\kilo\meter\per\hour}$ in $\si{\milli\meter\per\second}$ : $$\SI[per-mode=fraction]{0,018}{\kilo\meter\per\hour} = \num{0,018}\cdot\frac{\SI{1000}{\meter}}{\SI{3600}{\second}} = \num{18e-3}\frac{\SI{10}{\meter}}{\SI{36}{\second}} = \SI[per-mode=fraction]{5,0}{\milli\meter\per\second} \; .$$

   Einen Druck von $\SI{1013}{\hecto\pascal}$ in $\si{\pascal}$ : $$\SI{1013}{\hecto\pascal} = \num{1013}\cdot\SI{100}{\pascal} = \num{1,013}\cdot\SI{1e05}{\pascal} \; .$$

   Eine Beschleunigung von $17 \; {\text{g}}$ in $\si{\meter\per\square\second}$:

   Die Erdbeschleunigung beträgt $g = \SI[per-mode=symbol]{9,81}{\meter\per\square\second}$. In der Aufgabenstellung wird dieser Wert als Einheit der Beschleunigung interpretiert, was durch das nicht kursiv geschriebene "g" symbolisiert wird. Somit $$17 \cdot \SI{9,81}{\meter\per\square\second} = \SI{167}{\meter\per\square\second} \; .$$

2. Eine Leistung von $\SI{1800}{\kilo\joule\per\hour}$ in $\si{\watt}$: $$\SI[per-mode=fraction]{1800}{\kilo\joule\per\hour} = \num{1800} \cdot \frac{\SI{1000}{\joule}}{\SI{3600}{\second}} = \SI{500}{\watt} \; .$$

   Ein Druck von $\SI{2}{\kilo\newton\per\milli\meter\squared}$ in $\si{\pascal}$: $$\SI[per-mode=fraction]{2}{\kilo\newton\per\milli\meter\squared} = \num{2}\cdot\frac{\SI{1000}{\newton}}{(\SI{1e-03}{\meter})^2} = \num{2}\cdot\frac{\SI{1000}{\newton}}{\SI{1e-06}{\square\meter}} = \SI{2e09}{\pascal} \; .$$

   Eine Arbeit von $\SI{98}{\kilo\watt\hour}$ in $\SI{1}{\mega\joule}$: $$\SI[per-mode=fraction]{98}{\kilo\watt\hour} = \num{98}\cdot\SI{1e03}{\watt} \cdot \SI{1}{\hour} = \num{98}\cdot\SI{1e03}{\joule\per\second} \cdot \SI{3600}{\second} = \num{353}\cdot\SI{1e06}{\joule} = \SI{353}{\mega\joule} \; .$$

Ergänzungen

Diese Art von Umrechnungen sollte unbedingt erlernt werden:

• Umrechnungen mit Vorsilben (Präfixen), auch mit Potenzen,

• Umrechnungen mit den zugelassenen Einheiten $\si{\minute}$ und $\si{\hour}$.

Da Beschleunigungen manchmal vereinfachend als Vielfache der Erdbeschleunigung angegeben werden - etwa bei Crashtests - wurde eine entsprechende Umrechnung hier mit aufgenommen.

Erwartungshorizont Einheitenkonversion (K)

Dichte von Wasser von $\SI{1}{\kilo\gram\per\litre}$: $$\SI[per-mode=fraction]{1}{\kilogram\per\litre} = 1 \frac{\SI{1}{\kilogram}}{\SI{1}{\deci\meter\cubed}} = 1 \frac{\SI{1}{\kilogram}}{(\SI{0,1}{\meter})^3} = 1 \frac{\SI{1}{\kilogram}}{\SI{0,001}{\cubic\meter}} = 1000 \frac{\SI{1}{\kilogram}}{\SI{1}{\cubic\meter}} \; .$$

Eine Energie von $\SI{10}{\kilo\watt\hour}$: $$\SI{10}{\kilo\watt\hour} = \SI[per-mode=fraction]{10e3}{\joule\per\second}\cdot\SI{3600}{\second} = \SI[per-mode=fraction]{1e4}{\joule}\cdot\num{3,6e3} = \SI[per-mode=fraction]{3,6e7}{\kilogram\square\meter\per\square\second} \; .$$

Eine Kraft von $\SI{120}{\newton}$:

Für die Kraft gilt $F = m \cdot a$, somit $$\SI{120}{\newton} = \SI[per-mode=fraction]{120}{\kilogram}\cdot\SI{1}{\meter\per\square\second} = \SI[per-mode=fraction]{120}{\kilogram\meter\per\square\second} \; .$$

Ergänzungen

Nach der Norm DIN 1301-1 Einheiten - Teil 1: Einheitennamen, Einheitenzeichen können für die Angabe eines Volumens in Liter die folgenden, gleichberechtigten Einheitenzeichen verwendet werden: $\si{\litre}$, $\si{\liter}$.

Also $\SI{1}{\litre} = \SI{1}{\deci\meter\cubed} = \SI{1}{\liter}$.

Erwartungshorizont Sortierung nach Größe

$\SI{1}{\micro\meter}$, $\SI{1e-3}{\meter}$, $\SI{1}{\centi\meter}$, $\SI{2e-2}{\meter}$, $\SI{30}{\milli\meter}$, $\SI{1e2}{\meter}$, $\SI{1}{\kilo\meter}$, $\SI{1e6}{\meter}$.

Ergänzungen

Für die Sortierung ist es hilfreich, die Längen in wissenschaftlicher Notation ohne Präfixe zu schreiben:

$\SI{1}{\micro\meter}$	=	$\SI{1e-6}{\meter}$
$\SI{1e-3}{\meter}$	=	$\SI{1e-3}{\meter}$
$\SI{1}{\centi\meter}$	=	$\SI{1e-2}{\meter}$
$\SI{2e-2}{\meter}$	=	$\SI{2e-2}{\meter}$
$\SI{30}{\milli\meter}$	=	$\SI{3e-2}{\meter}$
$\SI{1e2}{\meter}$	=	$\SI{1e2}{\meter}$
$\SI{1}{\kilo\meter}$	=	$\SI{1e3}{\meter}$
$\SI{1e6}{\meter}$	=	$\SI{1e6}{\meter}$

Erwartungshorizont Einheiten (K)

$\beta$:	$\si{\per\square\second}$	…da das Argument des Kosinus dimensionslos (Einheit 1) sein muss.
$\gamma$:	$\si{\second}$	…damit sich für die Geschwindigkeit $\si{\meter\per\second}$ ergibt. Der Kosinus selbst ist dimensionslos mit einem Wert zwischen $-1$ und $1$.
$\delta$:	$\si{\meter}$	…damit der zweite Summand ebenfalls die Einheit $\si{\meter\per\second}$ hat.

Erwartungshorizont Einheitensystem

1. Die Einheiten der kinematischen Größen $v$ und $a$ wären: $$[v] = \frac{[x]}{[t]} = \SI{1}{Ga \per Na} \quad \text{und}$$ $$[a] = \frac{[v]}{[t]} = \SI{1}{Ga \per Na^2} \;.$$

2. Die Einheit der Kraft wäre: $$[F] = [m] \cdot [a] = \SI{1}{{Ob}~{Ga} \per Na^2} \; .$$

Ergänzungen

Konventionsgemäß bedeutet ein Größensymbol in eckigen Klammern die Einheit der betreffenden physikalischen Größe. So steht zum Beispiel $[F]$ nicht für die Kraft selbst, sondern für die Einheit der Kraft, also Newton oder kurz $\SI{1}{\newton}$.

Für die Geschwindigkeit sollte der Zusammenhang "Weg pro Zeit" genutzt werden, hier also Galilei pro Napoleon.

Für die Beschleunigung kann eine der angegebenen Beziehungen nach $a$ aufgelöst werden, $a = v / t$ und $a = 2 \cdot x / t^2$ liefern gleichermaßen für die Einheit Galilei pro Quadrat-Napoleon.

Für die Bestimmung der Einheit der Kraft muss eine Beziehung bekannt sein, die ihren Zusammenhang mit anderen Größen beschreibt. Aus der Mechanik ist bekannt "Kraft gleich Masse mal Beschleunigung" . Zu der Einheit der Beschleunigung kommt also die Einheit Obelix für die Masse als Faktor hinzu.

Erwartungshorizont Einheitenanalyse

Beschleunigung mal Zeit ergibt die SI‐Einheit $\si{\meter\per\second}$ und damit keine Strecke, sondern eine Geschwindigkeit. Der zweite Summand Geschwindigkeit mal Zeit hat zwar die richtige SI‐Einheit Meter; man kann aber keine zwei Terme mit unterschiedlichen Einheiten addieren.

Erwartungshorizont Vektorgrößen

Größe	v	s	Größe	v	s
Masse		$\times$	Geschwindigkeit	$\times$
Kinetische Energie		$\times$	Lageenergie		$\times$
Gravitationskraft	$\times$		Coulombkraft	$\times$
Impuls	$\times$		Druck		$\times$
Temperatur		$\times$	Wärme		$\times$

Erwartungshorizont Überlagerung

1. In der folgenden Skizze ist die Geschwindigkeit des Ruderboots relativ zum Fluss nach rechts und die Geschwindigkeit der Strömung nach unten dargestellt. Der Fluss ströme dabei über seine gesamte Breite hinweg mit gleicher Geschwindigkeit. Der schräge Pfeil zeigt die resultierende Geschwindigkeit als Überlagerung, das heißt als Vektorsumme.

   

2. $$v = \sqrt{v_{\mathrm{R}}^2 + v_{\mathrm{S}}^2} = \SI{5}{\meter\per\second} \; .$$

3. Der Tangens des Winkels ist das Verhältnis von Gegenkathete und Ankathete: $\tan(\alpha) = \frac{v_{\mathrm{S}}}{v_{\mathrm{R}}} = \frac{4}{3}$. In Gradmaß ergibt sich $\alpha = \arctan\left(\frac{4}{3}\right) \approx \SI{53,1}{\degree}$.

4. Die Überfahrt verlängert sich zeitlich nicht, da nur der Anteil $\vec{v}_{\mathrm{R}}$ die Zeitdauer bestimmt. Es gibt aber einen räumlichen Versatz am gegenüberliegenden Ufer.

Erwartungshorizont Kräfte

1. Keine Bewegung des Seils bedeutet, dass seine Beschleunigung $a$ gleich Null ist. Wegen $F = m \cdot a$ beträgt die resultierende Kraft dann $F = \SI{0}{\newton}$. Insgesamt ziehen $F_{\mathrm{M}} + F_{\mathrm{J}} = \SI{340}{\newton}$ nach links und ohne Anton $F_{\mathrm{T}} + F_{\mathrm{L}} = \SI{300}{\newton}$ nach rechts. Also muss Anton mit $F_{\mathrm{A}} = \SI{40}{\newton}$ nach rechts ziehen.

2. In der folgenden Skizze sind die Kräfte als im Schwerpunkt $S$ angreifend eingezeichnet:

   

   Alternativ kann das Seil in die Skizze aufgenommen werden:

   

   Die Vektorsumme zu Null kann durch Aneinanderhängen der Pfeile gebildet werden:

   

Ergänzungen

Es handelt sich um ein näherungsweise eindimensionales Problem und die angegebenen Kräfte sind die Beträge der Kraftkomponenten in Richtung des Seils. Die Kräftebilanz für die Beträge lautet $$F_{\mathrm{M}} + F_{\mathrm{J}} = F_{\mathrm{T}} + F_{\mathrm{L}} + F_{\mathrm{A}} \, .$$ Die Kräftebilanz für die vorzeichenbehafteten Komponenten beziehungsweise die Kräftevektoren lauten $$\begin{aligned} F_{\mathrm{M}} + F_{\mathrm{J}} + F_{\mathrm{T}} + F_{\mathrm{L}} + F_{\mathrm{A}} &= 0 \, , \\ \vec{F}_{\mathrm{M}} + \vec{F}_{\mathrm{J}} + \vec{F}_{\mathrm{T}} + \vec{F}_{\mathrm{L}} + \vec{F}_{\mathrm{A}} &= \vec{0} \, .\end{aligned}$$

Erwartungshorizont Masse und Gewicht

1. Die Gewichtskraft bezeichnet die Kraft, die ein Körper im Schwerefeld eines Himmelskörpers erfährt.

   Die Masse ist eine Eigenschaft eines Körpers, die nicht von dem Ort abhängt.

   An einem festen Ort auf der Erde sind die Gewichtskraft $F_\mathrm{G}$ und die Masse $m$ proportional zueinander, die Proportionalitätskonstante $g$ ist die Erdbeschleunigung: $F_\mathrm{G} = m \cdot g$.

   Unabhängig vom Ort bedingt die Masse die Trägheit, mit der sich ein Körper einer Änderung der Bewegung widersetzt.

   Beispiel: Es anstrengender, mit einem schweren Fahrrad bergauf zu fahren und es braucht mehr Kraft, ein massiges Fahrrad zu beschleunigen.

2. Die Masse eines Gegenstandes ist die gleiche auf der Erde und auf dem Mond.

   Die Gewichtskraft eines Gegenstandes auf dem Mond beträgt etwa ein Sechstel des Wertes auf der Erde, aber auch auf der Erde ist die Gewichtskraft eines Körper nicht an jedem Ort genau gleich.

Ergänzungen

Dass trotz der alltagssprachlichen Bezeichnungen ein Unterschied zwischen Masse und Gewichtskraft besteht, sollte bekannt sein. So gibt es ja schon einen Unterschied bezüglich des Vektorcharakters, der in G9 abgefragt wird. Eine Unterscheidung zwischen träger und schwerer Masse wäre wünschenswert.

Bezüglich des Verhältnisses der Gewichtskraft auf der Erde und dem Mond sollte zumindest bekannt sein, dass die Gewichtskraft auf dem Mond deutlich kleiner ist als auf der Erde.

Dass auf der Erdoberfläche $g$ einen Wert von etwa $\SI{9,81}{\newton\per\kilo\gram}$ beziehungsweise $\SI{9,81}{\meter\per\square\second}$ hat und der genaue Wert vom Ort abhängt, wäre gut zu wissen. Eine Kenntniss der Zusammenhänge zum Beispiel mit der Form der Erde, der Dichteverteilung oder dem rotatorischen Anteil geht über das Erwartbare hinaus.

Erwartungshorizont Aktionsprinzip

Wenn man eine Kraft auf einen Körper ausübt, wird dieser je nach Masse beschleunigt, eine große Masse weniger, eine kleine Masse mehr.

Beispiel: Anschieben eines Einkaufswagens. Je mehr er beladen ist, desto langsamer gewinnt er an Geschwindigkeit bei gleich starkem Anschieben.

Erwartungshorizont Newton

Die richtige Antwort ist [agNewtonRichtige], denn $F = m \cdot a$ umgestellt auf $a = F / m$ ergibt: $$a = \frac{\SI{1}{\newton}}{\SI{1}{\kilogram}} = \SI{1}{\meter\per\square\second} \; .$$

Erwartungshorizont Rutschvorgang (K)

Die Gleitreibung des Päckchens ist eine Kraft entgegen der Bewegungsrichtung und in diesem Fall groß genug, das Päckchen auf der zur Verfügung stehenden Strecke auf die Geschwindigkeit Null abzubremsen. Die Gleitreibungskraft muss also vom Betrag her größer als die Hangabtriebskraft sein. Nach dem Anhalten des Päckchens wirkt die Haftreibungskraft, die in diesem Fall die Hangabtriebskraft gerade kompensiert.

Erwartungshorizont Geschwindigkeits-Zeit-Diagramm

1. Der Körper bewegt sich von $t_0$ bis $t_1$ gleichförmig, also mit konstanter Geschwindigkeit. Danach wird er ab $t_1$ gleichmäßig verzögert, bis er sich zwischen $t_1$ und $t_2$ kurzzeitig in Ruhe befindet, $v = 0$. Dann wird er weiter, ohne Unterbrechung, in Gegenrichtung zur ursprünglichen Bewegungsrichtung mit der gleichen Kraft beschleunigt. Die Änderung der Geschwindigkeit zeigt jetzt in die gleiche Richtung wie die Geschwindigkeit und der Körper bewegt sich im Vergleich zur bisherigen Bewegung rückwärts. Anschließend wird er von $t_2$ bis $t_3$ gleichmäßig verzögert, bis er sich in Ruhe befindet. Der Betrag der dabei wirkenden verzögernden Beschleunigung ist kleiner als der Betrag der Beschleunigung im zweiten Zeitabschnitt, vgl. "Steigung im $v$-$t$-Diagramm entspricht der Beschleunigung".

2. Skizze der Beschleunigung als Funktion der Zeit:

   

Erwartungshorizont Dichte

Die Dichte ist definiert als "Masse pro Volumen": $\varrho= m / V$. Da alle Kugeln die gleiche Masse haben, muss die Kugel mit dem kleinsten Volumen die größte Dichte haben und umgekehrt, also gilt $$\varrho_P < \varrho_Q < \varrho_S < \varrho_R\,.$$

Erwartungshorizont Weg-Zeit-Diagramm

1. Weg‐Zeit‐Diagramm:

   Geg.:	Lisa:	$s_{\mathrm{L}0} = \SI{0}{\meter}$		$v_{\mathrm{L}} = \SI{4,00}{\meter\per\second}$
   	Anja:	$s_{\mathrm{A}0} = \SI{5,00}{\meter}$		$v_{\mathrm{A}} = \SI{3,50}{\meter\per\second}$

   Die Geschwindigkeiten entsprechen den Steigungen im Weg-Zeit-Diagramm, die Startpositionen den Achsenabschnitten auf der Weg-Achse:

   

2. Ja, Lisa schafft es, Anja innerhalb der ersten $\SI{50,0}{\meter}$ einzuholen. Nach $\SI{10,0}{\second}$ hat Lisa mit $\SI{40,0}{\meter}$ zurückgelegter Strecke den Vorsprung eingereicht.

   Mögliche Lösungswege:

   1. Anja hat $\SI{5,00}{\meter}$ Vorsprung, Lisa schafft pro Sekunde $\SI{0,500}{\meter}$ mehr, braucht also $\SI{10,0}{\second}$ zum Aufholen.

   2. Formale Rechnung: $$\begin{aligned} s_{\text{L}} &= v_{\text{L}} \cdot t \; ;\\ s_{\text{A}} &= v_{\text{A}} \cdot t + s_{\text{A}0} \; .\end{aligned}$$ Gleichsetzen ergibt $t_1 = \SI{10,0}{\second}$ und $s_1 = \SI{40,0}{\meter}$ für beide.

Erwartungshorizont Fallbewegung (K)

1. Berechnung für die vollständige Umwandlung von Lageenergie in kinetische Energie: $$\begin{aligned} E_{\mathrm{pot}} &= E_{\text{kin}} \; \\ m \cdot g \cdot \Delta h &= \frac{1}{2} \cdot m \cdot v^2 \; \\ v &= \sqrt{2 \cdot g \cdot \Delta h} \\ &= \SI{845}{\meter\per\second} \\ &\approx \SI{3000}{\kilo\meter\per\hour} \; .\end{aligned}$$

2. Seine gemessene Geschwindigkeit ist mit $v_{\mathrm{Messung}} = \SI{1357,6}{\kilo\meter\per\hour}$ weniger als die Hälfte des oben errechneten Wertes. Der große Unterschied lässt sich vor allem durch die in der Rechnung nicht berücksichtigte Luftreibung erklären.

Ergänzungen

Die Abnahme der Erdbeschleunigung mit der Höhe spielt hier eine untergeordnete Rolle. Das Verhältnis der Erdbeschleunigung in der Höhe $h$ über der Erde zu dem Wert auf dem Erdboden kann mit dem Erdradius $r_{\mathrm{E}}$ zu $g(r_{\mathrm{E}} + h) / g(r_{\text{E}}) \approx 1 / ( 1 + 2 \cdot h / r_{\text{E}})$ abgeschätzt werden und hat mit $\SI{39}{\kilo\meter}$ und $\SI{6400}{\kilo\meter}$ knapp den Wert $\num{0,99}$. Wird bei dieser Aufgabe der Wert der Erdbeschleunigung auf der Absprunghöhe mit $\num{0,99}\cdot\SI{9,81}{\meter\per\square\second} \approx \SI{9,71}{\meter\per\square\second}$ berechnet wird klar, dass das Ergebnisse unserer Berechnung mit einem festen Wert für $g$ mit höchstens zwei Ziffern angegeben werden sollte. Die fünf Ziffern bei der Fallhöhe und Geschwindigkeit deuten auf extrem genaue Messungen hin.

Erwartungshorizont Schwingung

1. $\hat{x} = \SI{10,0}{\centi\meter}$ und $f = 1 / \SI{0,500}{\second} = \SI{2,00}{\hertz}.$

2. Elongation über Zeit

   

3. Zum Zeitpunkt $t_2 = \SI{0,750}{\second}$ befindet sich die Kugel nach anderthalb Periodendauern im zweiten unteren Umkehrpunkt bei $\SI{-10,0}{\centi\meter}$.

Erwartungshorizont Beschleunigung

Da die Bewegung des Fußgängers sicher nicht exakt wie in dem schematischen Diagramm verläuft, wird hier das Ergebnis nur auf eine Stelle genau angegeben.

1. Die hier abschnittsweise konstante Beschleunigung entspricht der Steigung im $v$-$t$-Diagramm. Für die konstante Beschleunigung aus der Ruhe beim Zeitpunkt $t_0 = \SI{0}{\second}$ auf die Geschwindigkeit $v_1$ zum Zeitpunkt $t_1 = \SI{2}{\second}$ ergibt sich der Wert $$a_1 = \frac{v_1}{t_1 - t_0} = \frac{\SI{4}{\meter\per\second}}{\SI{2}{\second}} = \SI{2}{\meter\per\square\second}\, .$$ Nach dem Zeitpunkt $t_1$ ist die Beschleunigung konstant Null: $$a_2 = \SI{0}{\meter\per\square\second}\, .$$

2. Während der ersten Zeitspanne $t_1 - t_0 = t_1 = \SI{2}{\second}$ legt der Fußgänger bei gleichmäßiger Beschleunigung aus der Ruhe die Strecke $$s_1 = \frac{1}{2} \cdot a_1 \cdot t_1^2 = \frac{1}{2} \cdot \SI{2}{\meter\per\square\second} \cdot (\SI{2}{\second})^2 = \frac{1}{2} \cdot \SI{2}{\meter\per\square\second} \cdot \SI{4}{\square\second} = \SI{4}{\meter}$$ zurück. In der nachfolgenden Zeitspanne von $t_2 - t_1 = \SI{2}{\second}$ Dauer kommen bei gleichförmiger Bewegung $$s_2 = v_1 \cdot (t_2 - t_1 ) = \SI{4}{\meter\per\second}\cdot \SI{2}{\second} = \SI{8}{\meter}$$ hinzu. Die insgesamt zurück gelegte Wegstrecke beträgt also $$s_{\mathrm{ges}} = s_1 + s_2 = \SI{12}{\meter}.$$

3. Grafisch lässt sich die zum Zeitpunkt $t_2 = \SI{4}{\second}$ zurückgelegte Wegstrecke als "Fläche $A_{\mathrm{ges}}$" im $v$-$t$-Diagramm bestimmen:

   

   mit $A_1 = (1/2) \cdot \SI{2}{\second} \cdot \SI{4}{\meter\per\second} = \SI{4}{\meter}$, $A_2 = \SI{2}{\second} \cdot \SI{4}{\meter\per\second} = \SI{8}{\meter}$ und daraus $A_{\mathrm{ges}} = A_1 + A_2 = \SI{12}{\meter}$.

Ergänzungen

Die gleichfömige Bewegung kann auch als "Bewegung mit konstanter Geschwindigkeit" bezeichnet werden.

Die gleichmäßig beschleunigte Bewegung bei kann auch als "Bewegung mit konstanter Beschleunigung" bezeichnet werden.

Erwartungshorizont Weg-Zeit-Diagramme

Die Geschwindigkeit entspricht der Steigung im $x$-$t$-Diagramm.

1. Vergleich der Geschwindigkeiten $v_1 = v(t_1)$ und $v_2 = v(t_2)$:

   1. $v_1 > v_2$ ,

   2. $v_1 = v_2$ ,

   3. $v_1 < v_2$ ,

   4. $v_1 > v_2$ .

2. Vergleich der Geschwindigkeitsbeträge $|v_1|$ und $|v_2|$:

   1. $|v_1| > |v_2|$ ,

   2. $|v_1| = |v_2|$ ,

   3. $|v_1| > |v_2|$ ,

   4. $|v_1| < |v_2|$ .

Erwartungshorizont Geschwindigkeits-Zeit-Diagramme

Diagramm (B) erfüllt die Voraussetzungen für $v_y(t)$:

Positive Anfangsgeschwindigkeit (nach oben), Umkehrpunkt ganz oben, Symmetrie der Auf‐ und Abwärtsbewegung, linearer Geschwindigkeitsverlauf $\Rightarrow$ erfüllt konstante Erdbeschleunigung.

Diagramm (D) erfüllt die gleichförmige Bewegung für $v_x(t)$:

Konstante und positive Geschwindigkeit über den gewünschten Zeitraum.

Erwartungshorizont Parallelfahrt

1. An den Schnittpunkten der beiden Graphen befinden sich die Fahrzeuge "am gleichen Ort", sind also gleichauf.

2. F2 fährt rückwärts in dem Zeitraum mit negativer Steigung bis zum Minimum der Kurve. Da F1 sich mit konstanter Geschwindigkeit in die andere Richtung bewegt (positive Steigung des Graphen), bewegen sich die beiden Fahrzeuge in dieser Zeit entgegengesetzt.

3. Ungefähr ein Kästchen rechts vom Minimum hat der Graph F2 die gleiche Steigung wie der Graph von F1, also haben beide auch die gleiche Geschwindigkeit.

4. F1 fährt gleichförmig, hat also immer seine höchste Geschwindigkeit. F2 erreicht seine höchste Geschwindigkeit am Ende des Beobachtungszeitraums.

5. Die Fahrzeuge sind am Punkt der gleichen Geschwindigkeit aus [agParallelfahrtGleichesV] am weitesten voneinander entfernt (Visualisierung: Vertikaler Abstand der Funktionswerte, oder Erklärung über Geschwindigkeitsunterschied knapp vorher und knapp nach diesem Zeitpunkt - Extrempunkt in der Differenzfunktion, da Ableitung dort null).

Erwartungshorizont Berechnungen

Annas Lösung ist falsch: Sie hat mit einer gleichförmigen Bewegung gerechnet, obwohl diese in Wirklichkeit gleichmäßig beschleunigt ist. Außerdem hat sie die Erdbeschleunigung (den Ortsfaktor) mit der Geschwindigkeit verwechselt.

Bibis Lösung ist richtig: Sie hat mit dem Erhaltungssatz für die mechanische Energie gerechnet, dem zufolge die beim Start vorhandene Lageenergie vollständig in Bewegungsenergie umgewandelt wird. Diese Rechnung liefert nur eine Aussage über den Betrag der Geschwindigkeit. Das Vorzeichen der Geschwindigkeit könnte positiv oder negativ sein. Es steht für die Bewegungsrichtung und kann aus dieser Berechnung allein, ohne Festlegung eines Koordinatensystems, nicht bestimmt werden.

Clemens’ Lösung ist ebenfalls richtig: Sehr gut ist dabei seine Skizze, aus der hervorgeht, wie die Höhenwerte entlang der von ihm festgelegten Koordinatenachse ansteigen. Zur Berechnung verwendet er dann die Bewegungsgleichung und erhält so das korrekte negative Vorzeichen der Geschwindigkeit, das die Bewegungsrichtung "nach unten" bezüglich dieser Achse beschreibt.

Erwartungshorizont Treppensteigen

Die Aufgaben a), b) und c) sind lösbar.

Bei d) und e) fehlen jeweils Angaben zu der für das Hinaufsteigen benötigten Zeit, die Aufgabe e) macht das nochmals besonders deutlich.

Die Ergebnisse - soweit berechenbar - im Einzelnen:

1. Jan und Max steigen beide die gleiche Höhe von $h = \SI{15,0}{\meter}$ hinauf. Ihre Massen unterscheiden sich. Dies ist in der Skizze angedeutet.

   

   Die Lageenergie berechnet sich aus $E_{\mathrm{Lage}} = m \cdot g \cdot h$. Dies ergibt für die beiden Jungen $$E_{\mathrm{Jan}} = m_{\mathrm{Jan}} \cdot g \cdot h = \SI{35,0}{\kilo\gram} \cdot \SI{9,81}{\meter\per\square\second} \cdot \SI{15,0}{\meter} = \SI{5,15}{\kilo\joule} \; .$$ und $$E_{\mathrm{Max}} = m_{\mathrm{Max}} \cdot g \cdot h = \SI{40,0}{\kilo\gram} \cdot \SI{9,81}{\meter\per\square\second} \cdot \SI{15,0}{\meter} = \SI{5,89}{\kilo\joule} \; .$$

2. Die Murmeln fallen die gleiche Strecke $h$ und treffen gleichzeitig auf dem Boden auf. Unter Vernachlässigung der Luftreibung folgt die Auftreffgeschwindigkeit $v_{\mathrm{Boden}}$ aus dem Energieerhaltungssatz, die Masse $m$ der Murmeln ist dabei unerheblich: $$E_{\mathrm{pot}} = m \cdot g \cdot h =\frac{1}{2} \cdot m \cdot v_{\mathrm{Boden}}^2 = E_{\mathrm{kin}} \; .$$ Daraus $$v_{\mathrm{Boden}} = \sqrt{ 2 \cdot g \cdot h } = \sqrt{ 2 \cdot \SI{9,81}{\meter\per\square\second} \cdot \SI{15,0}{\meter} } = \SI{17,2}{\meter\per\second} \; .$$

3. Die Fallzeit $t_{\mathrm{Max}}$ der Murmel von Max berechnet sich aus: $$h = \frac{1}{2} \cdot g \cdot t_{\mathrm{Max}}^2$$ zu $$t_{\mathrm{Max}} = \sqrt{ 2 \cdot h / g} = \sqrt{ 2 \cdot \SI{15,0}{\meter} / \SI{9,81}{\meter\per\square\second}} = \SI{1,75}{\second} \; .$$ Die Fallzeit $t_{\mathrm{Jan}}$ der Murmel von Jan soll mindestens $\SI{0,3}{\second}$ größer sein. Also $t_{\mathrm{Jan}} > t_{\mathrm{Max}} + \SI{0,3}{\second} = \SI{2,05}{\second}$. Somit $$t_{\mathrm{Jan}} = \sqrt{ 2 \cdot h_{\mathrm{Jan}} / g} > \SI{2,05}{\second} \quad \text{daraus}$$ $$h_{\mathrm{Jan}} > \frac{1}{2} \cdot \SI{4,2025}{\second\squared} \cdot g \;$$ $$h_{\mathrm{Jan}} > \frac{1}{2} \cdot \SI{4,2025}{\second\squared} \cdot \SI{9,81}{\meter\per\square\second} = \SI{20,6}{\meter} \; .$$ Jan müsste also mindestens $h_{\mathrm{Jan}} - h = \SI{5,6}{\meter}$ weiter nach oben steigen als Max. Da die Höhe der Stockwerke in Jans Haus nur $\SI{2,5}{\meter}$ beträgt, bedeutet dies weitere drei Stockwerke Aufstieg.

4. Die mechanische Leistung $P$ berechnet sich allgemein aus der in einer Zeitspanne $\Delta t$ aufgebrachten Arbeit $\Delta W$ zu $P = \Delta W / \Delta t$. Im Fall von Jan und Max wäre diese Zeitspanne die jeweilige Dauer des Aufstiegs, die jedoch nicht angegeben ist.

5. Dass keine Zeitangaben vorliegen, wird hier nochmals deutlich.

Erwartungshorizont Aufgabenstellung

1. Es wird sich um den senkrechten Wurf eines Körpers nach oben handeln. Die Startgeschwindigkeit ist dabei $v_0$ und der Startpunkt liegt in einer Höhe $h$ über dem Erdboden. Auf den Körper wirkt die Schwerkraft $F_{\mathrm{G}}$.

2. Daraus könnten verschiedene Größen berechnet werden:

   • Flugdauer bis zum Erreichen des höchsten Punkts,

   • Flugdauer bis zum Aufprall auf dem Erdboden,

   • maximale Steighöhe,

   • Aufprallgeschwindigkeit am Boden,

   • Masse des Körpers,

   • Steighöhe mit halber kinetischer Energie oder halber Startgeschwindigkeit,

   • …

Erwartungshorizont Dichtebestimmung

Sollten die folgenden Formeln oder Dichtebereiche nicht bekannt sein, sind diese zuerst nachzuschlagen.

1. Mit den Formeln für das Volumen von Kreiskegel und Zylinder $$\begin{aligned} V &= \frac{1}{3} \cdot\pi \cdot r^2 \cdot h + \pi \cdot r^2 \cdot h \\ &= \frac{4}{3} \cdot\pi \cdot r^2 \cdot h \\ &= \frac{4}{3} \cdot\pi \cdot \left(\SI{0,5}{\deci\meter}\right)^2 \cdot \SI{1}{\deci\meter} \\ &= \SI{1,047}{\litre} \\\end{aligned}$$ folgt die Dichte $$\begin{aligned} \varrho&= \frac{m}{V}\\ &= \frac{\SI{1}{\kilogram}}{\SI{1,047}{\litre}} \\ &= \SI{955}{\kilogram\per\cubic\meter} \; .\end{aligned}$$

2. Der Körper wird aus Holz oder Polyethylen bestehen. Polyethylen hat eine Dichte im Bereich von $\SI{870}{\kilogram\per\cubic\meter}$ bis $\SI{970}{\kilogram\per\cubic\meter}$. Die Dichte von Holz schwankt in einem großen Bereich, je nach Holzart und Feuchtigkeit.

Erwartungshorizont Zugfahrt

1. Geschwindigkeit $v(t)$: durchgezogene Kurve in der folgenden Skizze

2. Beschleunigung $a(t)$: gestrichelte Kurve in der folgenden Skizze

   

3. Die insgesamt zurückgelegte Strecke entspricht der schraffierten Fläche $s$ unter dem Verlauf von $v(t)$ im $v$-$t$-Diagramm zwischen Start- und Endzeitpunkt. Diese Fläche im Diagramm gilt es zu bestimmen. Im vorliegenden Fall lässt sie sich in einfache geometrische Komponenten - Rechtecke und Dreiecke - zerlegen, die ausgemessen, deren Flächenanteile dann berechnet und die am Ende aufsummiert werden. In Basiseinheiten hat diese Fläche dann die Einheit $[ v ] \cdot [ t ] = \si{\meter\per\second} \cdot \si{\second} = \si{\meter}$.

Erwartungshorizont Stoßvorgänge (K)

Für die Bewegung der Waggons wird Reibungsfreiheit angenommen.

1. Der vorliegende Stoß ist inelastisch. Die Waggons können nicht elastisch voneinander abprallen, sondern bleiben durch das Ankoppeln aneinander hängen. Dies kann als eine Art Verkeilen der Waggons ineinander aufgefasst werden.

2. Das Verkeilen kostet mechanische Energie. Somit bliebt während dieses Vorgangs die mechanische Energie nicht erhalten. Der Impulserhaltungssatz gilt dagegen, denn es wirken nur innere Kräfte zwischen den Waggons.

3. Aus dem Impulserhaltung folgt $$\begin{aligned} p_{\mathrm{vorher}} &= p_{\mathrm{nachher}} \; \\ M \cdot v + \frac{3}{2} \cdot M \cdot \frac{1}{2} \cdot v &= \left(M + \frac{3}{2} \cdot M\right) \cdot u \quad \text{daraus}\\ \frac{7}{4} \cdot v &= \frac{5}{2} \cdot u \; \\ u &= \frac{7}{10} \cdot v \; .\end{aligned}$$ Beide Waggons fahren nach dem Ankoppeln zusammen mit $\SI{70}{\percent}$ der Geschwindigkeit des zu Beginn schnelleren Waggons weiter.

Ergänzungen

Die Bezeichnung von Stoßvorgängen ist in der Literatur nicht einheitlich. Beim Stoß erfolgt in aller Regel eine Deformation der beiden Stoßpartner.

Ist diese Deformation vollkommen reversibel, geht also keinerlei mechanische Energie durch den Stoßvorgang verloren, liegt ein elastischer Stoß vor. Manchmal wird dieser auch als vollkommen elastisch oder kurz vollelastisch bezeichnet.

Werden die Stoßpartner bei dem Stoßvorgang bleibend deformiert, wird ein Teil der anfangs vorhandenen mechanische Energie in Deformationsarbeit verwandelt. Dann liegt ein unelastischer Stoß vor.

Bewegen sich die beiden Stoßpartner nach dem Stoß voneinander getrennt weiter, finden sich dafür oft die folgenden Bezeichnungen: anelastisch, inelastisch, teilelastisch, teilplastisch oder teilweise plastisch.

Der hier beschriebene Fall, dass die beiden Stoßpartner sich nach dem Stoß zusammen weiterbewegen, wird oft einfach als unelastisch oder plastisch, manchmal aber auch als vollkommen unelastisch, vollkommen plastisch oder vollplastisch bezeichnet.

Erwartungshorizont Schlauchstück

Der Außenradius des Schlauchstücks ist gleich dem halben Außendurchmesser: $r_{\text{au{\ss}en}} = d/2$. Für den Innenradius ist hiervon die Wandstärke abzuziehen.

1. Die Dichte ist der Quotient aus Masse $m$ und Volumen $V$. Sie wird zuerst in $\si{\gram\per\centi\meter\cubed}$ berechnet: $$\begin{aligned} V &= \pi \cdot \left( r_{\text{au{\ss}en}}^2 - r_{\mathrm{innen}}^2 \right) \cdot L\\ &= \pi \cdot \left( (\SI{1,0}{\centi\meter})^2 - (\SI{0,7}{\centi\meter})^2 \right) \cdot \SI{20}{\centi\meter}\\ &= \SI{32,04}{\centi\meter\cubed} \; ;\\ \varrho&= \frac{m}{V} = \frac{\SI{50}{\gram}}{\SI{32,04}{\centi\meter\cubed}} = \SI{1,56}{\gram\per\centi\meter\cubed} \\ &= \num{1,6} \cdot \frac{\SI{1e-03}{\kilo\gram}}{(\SI{1e-01}{\deci\meter})^3} = \num{1,6} \cdot \frac{\SI{1e-03}{\kilo\gram}}{\SI{1e-03}{\deci\meter}} = \SI{1,6}{\kilo\gram\per\deci\meter\cubed} \; .\end{aligned}$$

2. Das Schlauchstück wird im Öl nicht schwimmen. Seine Dichte von $\SI{1,6}{\gram\per\centi\meter\cubed}$ ist deutlich höher als die Dichte des Öls von $\SI{0,85}{\gram\per\centi\meter\cubed}$.

Ergänzungen

Damit ein Objekt in einer Flüssigkeit (einem Fluid) schwimmt, muss die darin auf das Objekt einwirkende Auftriebskraft seiner Gewichtskraft $F_{\mathrm{G}}$ das Gleichgewicht halten (Prinzip von Archimedes). Diese Auftriebskraft $F_{\mathrm{A}}$ ist wiederum gleich der Gewichtskraft des von dem Objekt verdrängten Flüssigkeitsvolumens $V_{\mathrm{Fluid}}$. Die Bedingung für Schwimmen ist, dass Kräftegleichgewicht herrscht: $$F_\mathrm{G} = \varrho_{\mathrm{Objekt}} \cdot V_{\mathrm{Objekt}} \cdot g = \varrho_{\mathrm{Fluid}} \cdot V_{\mathrm{Fluid}} \cdot g = F_\mathrm{A} \; .$$ Ein Objekt kann maximal, das heißt bei vollständigem Eintauchen, sein Eigenvolumen an Flüssigkeit verdrängen. Im Grenzfall gilt also $V_{\mathrm{Fluid}} = V_{\mathrm{Objekt}}$. Dann vereinfacht sich die Gleichgewichtsbedingung zu $\varrho_{\mathrm{Objekt}} = \varrho_{\mathrm{Fluid}}$. Sie ist im Fall des Schlauchstücks in Öl nicht erfüllt.

Erwartungshorizont Multimeter

1. Bei Messung 1 im linken Bild wird mit dem Multimeter eine Spannung gemessen, bei Messung 2 im rechten Bild ein Strom.

2. Messung 1 liefert einen Spannungswert von $\SI{-20,0}{\volt}$ (oder auch $\SI{20,0}{\volt}$). Ohne weitere Informationen über die Polung des Messgeräts in der Schaltung ist keine Aussage über das Vorzeichen und seine Bedeutung möglich. Messung 2 ergibt einen Stromwert von $\SI{5,0}{\ampere}$.

Ergänzungen

In diesem Multimeter dient ein analoges Zeigerinstrument zur Anzeige. Am Drehschalter wird der jeweils aktive Messbereich eingestellt. Der damit eingestellte Wert steht dabei für den Endwert der betreffenden Skala, also für den Vollausschlag des Zeigers. Bei der Ablesung ist zu beachten, dass je nach Messbereich besser die obere oder die untere Skala zu verwenden ist. In Messbereichen mit den Endwerten 300, 30, 3, ... wird sinnvollerweise auf der oberen Skala abgelesen während in den Messbereichen mit dekadischen Endwerten besser die untere Skala verwendet wird. Schließlich sind die beiden Skalen symmetrisch. Das heißt, sie haben die Null in der Mittelstellung, so dass das Messgerät unabhängig von seiner Polung in der Schaltung bis zum jeweiligen Endwert des Messbereichs eingesetzt werden kann.

Im linken Bild ist der Messbereich $\SI{30}{\volt}$ eingestellt. Demnach ist der Messwert auf der oberen Skala abzulesen, ihr Endwert $3$ entspricht also einem Messwert von $\SI{30}{\volt}$ für die Spannung. Der Zeiger steht in der linken Hälfte der Skala auf $2$, also formal bei $\SI{-20,0}{\volt}$.

Im rechten Bild ist der Messbereich $\SI{10}{\ampere}$ eingestellt. Demnach ist der Messwert auf der unteren Skala abzulesen, ihr Endwert $1$ entspricht also einem Messwert von $\SI{10}{\ampere}$ für den Strom. Der Zeiger steht bei $0,5$ in der rechten Hälfte der Skala, also formal bei $\SI{5,0}{\ampere}$.

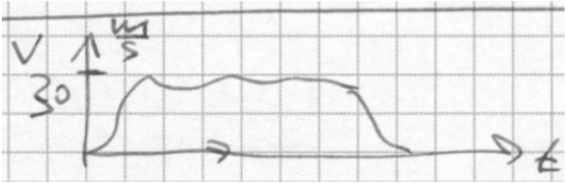
Erwartungshorizont Schulweg

Die Skala ist nicht plausibel, die Geschwindigkeit von etwa $\SI{30}{\meter\per\second}$, also umgerechnet über $\SI{100}{\kilo\meter\per\hour}$, ist beim Laufen nicht erreichbar.

Erwartungshorizont Schätzwert

Der Sinus schwankt zwischen $-1$ und $1$, ist also vernachlässigbar verglichen mit dem anderen Summanden. Es ist $\pi^2 \approx 10$. Mit diesen Näherungen und umgeschriebenen Zehnerpotenzen erhalten wir zunächst $$\begin{aligned} \frac{\num{0,037e29} \cdot \pi^2+\sin\left(\num{0,083e47}\right)}{\left(\num{0,00232e-22}\right)^2} &\approx \frac{\num{3,7e28}}{\left(\num{2,32e-25}\right)^2}\\ &= \frac{\num{3,7}}{\left(\num{2,32}\right)^2} \cdot \num{1e78} \; .\end{aligned}$$ Der letzte Bruch ist etwas kleiner als $4/2^2 = 1$ und deutlich größer als $\num{0,1} < 3/3^2$. Die Zahl ist also von der Größenordnung $10^{77}$.

Erwartungshorizont Weltbevölkerung (K)

Hier ist eine quantitative Abschätzung gefragt, keine exakte Berechnung ("Fermi-Problem). Wir gehen von stehenden Menschen aus, um möglichst wenig Fläche pro Person zu belegen. Ein erwachsener Mann hat eine Schulterbreite von etwa $\SI{40}{\centi\meter}$ und von Brust zu Rücken eine "Tiefe" von etwa $\SI{25}{\centi\meter}$. Damit benötigt er eine Standfläche von $\SI{0,1}{\square\meter}$. Mehr als zwei kleine Kinder passen sicherlich nicht auf diese Fläche. Die Weltbevölkerung wird der Einfachkeit halber auf 8 Milliarden geschätzt, ohne die Anteile von Kindern und Erwachsenen noch näher zu gewichten. Somit wird die abgeschätzte Fläche tendenziell eher zu hoch sein. Unter diesen Annahmen müsste der benötigte Kreis also eine Fläche von 800 Millionen $\si{\square\meter}$ aufweisen, das entspricht einem Radius von ziemlich genau $\SI{16}{\kilo\meter}$ oder einem Durchmesser von $\SI{32}{\kilo\meter}$.

Erwartungshorizont Schnappschuss

Der Fahrradfahrer hat wohl den üblichen Reifendurchmesser von 28 bis 29 Zoll oder ca. $\num{70}$ bis $\SI{75}{\centi\meter}$. Ziemlich genau ein Viertel dieses Durchmessers scheint er sich während der 1/50 Sekunde bewegt zu haben, d.h. in einer Sekunde das 50‐fache eines Viertels von $\SI{75}{\centi\meter}$ oder ca. $\num{9}$ bis $\SI{9,5}{\meter\per\second}$. Das entspricht etwa $\num{30}$ bis $\SI{35}{\kilo\meter\per\hour}$ und damit einer durchaus realistischen, wenn auch sportlichen Fahrradgeschwindigkeit.

Erwartungshorizont Tennisbälle

1. Ein ganz einfache Abschätzung ist über die Berechnung des Volumens von 200 Tennisbällen möglich:

   Ein Ball hat einen Durchmesser von etwa $\SI{7}{\centi\meter}$ und damit das Volumen $\frac{4}{3} \cdot \pi \cdot r^3 = \SI{179,6}{\centi\meter\cubed}$. Demnach haben 200 Bälle ein Volumen von $V_{200} = \SI{35919}{\centi\meter\cubed}$.

   Das Volumen der Kiste beträgt $V_{\mathrm{Kiste}} = A \cdot h$ und muss auf jeden Fall gleich dem Volumen der Bälle sein. Also ist $V_{\mathrm{Kiste}} = V_{200}$ und daraus folgt die erforderliche Höhe $h$ der Kiste zu $$h = \frac{V_{\mathrm{Kiste}}}{A} = \frac{V_{200}}{A} = \frac{\SI{35919}{\centi\meter\cubed}}{\SI{50}{\centi\meter} \times \SI{40}{\centi\meter}} = \SI{18,0}{\centi\meter} \; .$$

2. Eine etwas realistischere Abschätzung berücksichtigt den freien Raum zwischen den Bällen durch eine anschauliche Überlegung:

   Auf die $\SI{50}{\centi\meter}$ Länge der Grundfläche der Kiste passen etwa 7 Tennisbälle, auf die $\SI{40}{\centi\meter}$ Breite dann 5 oder im besten Fall 6 Reihen, wenn diese etwas ineinander greifen. Dies bedeutet etwa 40 Tennisbälle pro Schicht und damit werden insgesamt 5 Schichten benötigt, die wohl ebenfalls ein wenig ineinander greifen werden. Diese knapp 5 Tennisbälle entsprechen einer Höhe zwischen $\SI{30}{\centi\meter}$ und $\SI{35}{\centi\meter}$ für die Kiste.

3. Die Theorie der dichtesten Kugelpackung liefert eine Faustregel, der zufolge etwa $\SI{75}{\percent}$ oder 3/4 des erforderlichen Volumens von den Kugeln selbst eingenommen werden.

   Nach dieser Regel sollte die Kiste ein Volumen von $V_{200} / 0,75 = \SI{47892}{\centi\meter\cubed}$ haben. Geteilt durch ihre Grundfläche ergibt dies eine erforderliche Höhe von etwa $\SI{24}{\centi\meter}$.

Ergänzungen

Die Theorie der endlichen Kugelpackungen ist mathematisch recht anspruchsvoll…